§7.4
数量积 向量积 混合积
一
两向量的数量积
1 向量的数量积定义
设物体在常力![]() 的作用下沿直线从点
的作用下沿直线从点![]() 移到点
移到点![]() ,用
,用![]() 表示位移向量
表示位移向量![]() ,力
,力![]() 在位移方向
在位移方向![]() 上的分力大小为
上的分力大小为![]() ,力
,力![]() 所作的功为:
所作的功为:
![]()
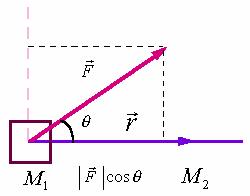
抛开这一问题的物理背景,我们可以给出一般地向量的数量积定义:
设![]()
![]() 是两向量,且它们之间的夹角为
是两向量,且它们之间的夹角为![]() ,称数量
,称数量![]() 为向量
为向量![]()
![]() 的数量积,并记作
的数量积,并记作 ![]() ,即
,即
![]()
注明:记号![]() 又可称之为“
又可称之为“![]() 点乘
点乘![]()
![]() ”。
”。
据此定义,上例所求的功![]() 实际上是力
实际上是力![]() 与位移
与位移![]() 的数量积,即
的数量积,即
![]() 。
。
因![]() 是
是![]() 在向量
在向量![]() 方向上的投影,若用
方向上的投影,若用![]() 来记这个投影,便有:
来记这个投影,便有:
![]()
类似有:![]()
这表明: 两向量的数量积等于其中一向量的模与另一向量在该向量方向上的投影的乘积。
这一事实的力学意义是十分鲜明的。
2、数量积的性质
(1)、![]()
事实上,![]() 与
与![]() 的夹角
的夹角![]() , 故
, 故
![]()
(2)、设![]() ,
,![]() 为非零向量,若
为非零向量,若![]() ,那么
,那么![]() 与
与![]() 垂直( 记作
垂直( 记作![]() );反之,若
);反之,若![]() ,那么
,那么![]() 。
。
证明: ![]()
![]()
(3)、(交换律)![]()
事实上,![]()
(4)、(分配律)![]()
事实上,
![]()
![]()
(5)、(数乘向量的结合律) ![]()
证明: 设向量![]() 与
与![]() 之间的夹角为
之间的夹角为![]() ,
,
若
![]() ,
,![]() 与
与![]() 同方向,故
同方向,故![]() 与
与 ![]() 的夹角仍为
的夹角仍为 ![]() ,于是
,于是
![]()
![]()
若
![]() ,
, ![]() 与
与![]() 反方向, 故
反方向, 故![]() 与
与 ![]() 的夹角仍为
的夹角仍为![]() , 于是
, 于是
![]()
![]()
若
![]() ,
,![]()
综合上述三点,有
![]() 成立。
成立。
类似地可证明
![]() 。
。
(6)、两向量数量积的坐标表示形式
设
![]() ,则有
,则有
![]()
证明:![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
注明:基本单位向量有 ![]()
利用向量数量积的计算公式,很容易地得到了下列向量模计算公式
![]()
(7)、两向量间夹角余弦的坐标表示式
若
![]() ,
,![]() ,由
,由 ![]() ,有
,有
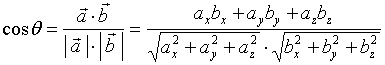
并且有
![]()
【例1】已知三点![]() ,
, ![]() 和
和![]() ,求向量
,求向量![]() 与
与![]() 之间的夹角
之间的夹角![]() 。
。
解:![]()
![]()
而
![]()
![]()
![]()
故
![]()
【例2】设液体流过平面![]() 上面积为
上面积为![]() 的一个区域,液体在该区域上各点处的流速均为常向量
的一个区域,液体在该区域上各点处的流速均为常向量![]() ,设
,设![]() 为垂直于
为垂直于![]() 的单位向量,计算单位时间内经过该区域流向
的单位向量,计算单位时间内经过该区域流向![]() 所指向一侧的液体重量
所指向一侧的液体重量![]() ( 设液体的比重为
( 设液体的比重为![]() )。
)。
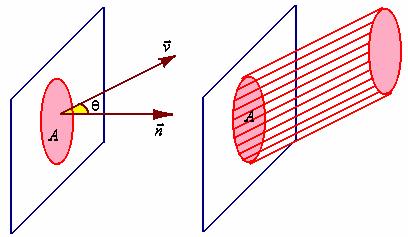
解:单位时间内流过区域的液体形成一个底面积为![]() ,斜高为
,斜高为![]() 的斜柱体, 且斜高与底面垂线的夹角即为向量
的斜柱体, 且斜高与底面垂线的夹角即为向量![]() 与
与![]() 之间的夹角
之间的夹角![]() 。
。
所以,该斜柱体的高为![]() ,即
,即![]() 在
在![]() 方向上的投影。
方向上的投影。
斜柱体的体积为
![]()
从而,单位时间内经过区域流向所指一方的液体重量为
![]()
很明显,若![]() ,即
,即![]() 垂直于平面
垂直于平面![]() 时,
时,![]()
这与我们直观的理解是一致的。

2、向量的数量积不具有结合律
一般情况下,![]() ,因此,写法
,因此,写法![]() 是无意义的。
是无意义的。
【反例】取
![]() ,
, ![]() ,
, ![]()
![]()
![]()
![]()
二 两向量的向量积
1、由力矩问题引入向量的向量积
设![]() 为一根杠杆的支点,有一个力
为一根杠杆的支点,有一个力![]() 作用于这杠杆上的点
作用于这杠杆上的点![]() 处,
处,![]() 与
与![]() 的夹角为
的夹角为![]() ,由力学知识可知,力
,由力学知识可知,力![]() 对支点
对支点![]() 的力矩是一个向量
的力矩是一个向量![]() ,它的模为
,它的模为 ![]()
![]()
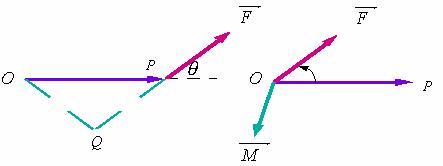
而方向垂直于![]() 与
与![]() 所决定的平面,其指向依右手规则来决定,即当右手的四个手指从
所决定的平面,其指向依右手规则来决定,即当右手的四个手指从![]() 以不超过
以不超过![]() 的转角转向
的转角转向![]() 握拳时,大拇指的指向就是力矩
握拳时,大拇指的指向就是力矩![]() 的指向。
的指向。
这类物理问题所反映出的数学运算便是我们要定义的向量间的向量积。
【定义】设向量![]() 由向量
由向量![]() 与
与![]() 依下列方式定出:
依下列方式定出:
![]() 的模为
的模为![]() , 其中
, 其中![]() 为向量
为向量![]() 与
与![]() 之间的夹角;
之间的夹角;
![]() 的方向垂直于
的方向垂直于![]() 与
与![]() 所决定的平面,
所决定的平面,![]() 的指向按右手规则从
的指向按右手规则从![]() 转向(转角小于
转向(转角小于![]() )
)![]() 来决定。
来决定。
那么称向量![]() 为向量
为向量![]() 与
与![]() 的向量积,记作
的向量积,记作![]() ,即
,即 ![]() 。
。
向量的向量积又常称作向量的叉乘,![]() 也常念作“
也常念作“ ![]() 叉乘
叉乘![]()
![]() ”。
”。
因此,上面的力矩![]() 等于
等于![]() 与力
与力![]() 的向量积,即
的向量积,即![]() 。
。
2、向量积的性质
(1)、![]()
(2)、对于非零向量![]() 与
与![]() ,
,![]() 与
与![]() 平行( 即
平行( 即![]() )的充要条件是
)的充要条件是![]() 。
。
(3)、设![]() ,
,![]() 为两个非零向量,模
为两个非零向量,模![]() 在几何上表示以
在几何上表示以![]() 与
与 ![]() 为边的平行四边形的面积。
为边的平行四边形的面积。


(5)、分配律 ![]()
![]()
(6)、设![]() ,
,![]() 为实数,则
为实数,则 ![]()
![]()
(7)、向量积的坐标表示式
设
![]() ,
,![]() ,则有
,则有
![]()
![]()
![]()
![]()

于是,有
![]()
![]()
为了便于记忆,我们引入形式化的三阶行列式的记法。
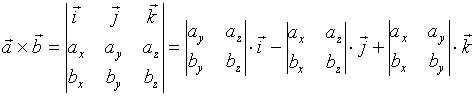
![]()
由向量的向量积坐标表示式,可给出两向量平行的充要条件的又一形式:
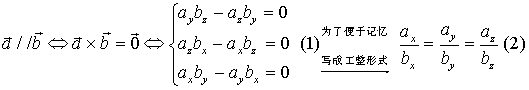
这一向量平行的对称式条件,当分母有为零的元素时,应依如下规则来理解它的意义:
(1)、当![]() 中仅有一个为零时,如
中仅有一个为零时,如 ![]()
则(1)式成为
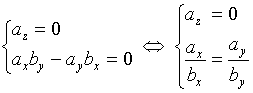
因此,
此时(2)式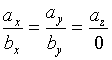 的意义应理解为
的意义应理解为
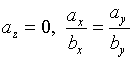
(2)、当![]() 中仅有二个为零时,如
中仅有二个为零时,如 ![]()
则(1)式成为 ![]()
因此,此时(2)式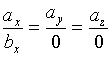 的意义应理解为
的意义应理解为
![]()
(3)、当 ![]() 时
时
则(1)式对于任意实数 ![]() 均成立
均成立
因此,此时(2)式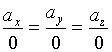 的意义为
的意义为
![]() 可取任意实数。
可取任意实数。
【例3】已知三角形![]() 的顶点是
的顶点是![]() ,
,![]() 和
和![]() ,求此三角形的面积
,求此三角形的面积![]() 。
。
解:![]()
![]()
![]()
![]()
![]()
![]()
![]()
而 ![]()
![]()
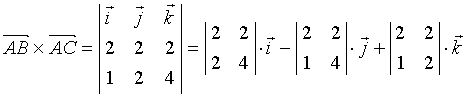
![]()
![]()
![]()
三 向量的混合积
1、平行六面体的体积
如图所示,以![]() ,
, ![]() 和
和![]() 为棱的平行六面体的体积
为棱的平行六面体的体积![]() ,
,
应为其底面积![]() 乘以高
乘以高![]() 。
。
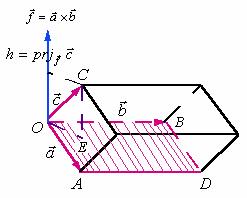
底面积为 ![]() ,由于高
,由于高![]() 垂直于底面
垂直于底面![]() ,它可以看作向量
,它可以看作向量![]() 在垂直于底面的向量
在垂直于底面的向量![]() 上的投影
上的投影 ![]() ,体积值
,体积值![]() 为
为
![]()
2、向量混合积定义
设有三个向量![]() ,
,![]() 与
与![]() ,先作
,先作![]() ,将向量
,将向量![]() 与
与![]() 作数量积
作数量积![]() ,这样得到的数量称作三向量
,这样得到的数量称作三向量![]() ,
,![]() ,
,![]() 的混合积,并记作
的混合积,并记作![]() 。
。
于是,平行六面体的体积为
![]()
3、向量混合积的计算
设![]() ,
,![]() ,
,![]() ,则
,则
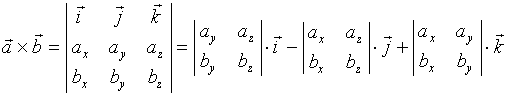
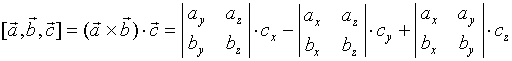

利用向量混合积的几何意义,我们可以得到一个十分有用的结论:
空间三向量![]() ,
,![]() 与
与![]() 共面的充要条件是
共面的充要条件是 ![]() 。
。